LAST week (February 20) the Office for National Statistics (ONS) published new estimates of excess deaths in the UK based on a revised methodology. The figures were greeted with some scepticism. Academics from the University of Oxford immediately warned that the new modelling revealed a major drop in expected deaths in 2020, ‘making it appear that far more people had died than normal during the first year of the pandemic’, as the Telegraph reported. The new modelling was also criticised for revising down excess deaths last year, ‘even though many charities and universities have reported unusually large upswings in mortality rates for conditions like heart disease‘. Indeed.
I too wondered how the ONS managed to ‘revise down’ excess deaths in 2023 and make them look so much fewer, so I decided to I run their model(s) independently and to conduct an independent re-analysis. What follows is that – and an explanation of how the trick is performed!
First I went to the link that describes the ONS methodology; then to this link which is the corresponding dataset; and finally to this link which is their R-based code.
I began by assuming the ONS dataset itself is reliable. However, it is possible to question the total population estimates within that dataset, especially in respect of immigration, including illegal immigration. Consequently, there may be a degree of underestimation of excess deaths on that basis. Nevertheless, the key issue relates to how the data are processed to provide ‘excess deaths’.
Giving public access to their code is unusual. Probably the ONS anticipated being deluged with hard questions from statistically competent people, and thought this is the best way of addressing such queries. This is welcome and sensible. However, I decided to use an independent code.
The key issue, as noted above, is that the new methodology estimates far smaller numbers of excess deaths in 2023 (though less so in 2020 and 2021, and actually rather more in 2022). Prior to carrying out any re-analysis, I thought about how this substantial change might have come about.
There are two factors which I suspect contribute. The first is the change in the UK’s age profile over the last 19 years. The ONS methodology statement summarises UK population changes between 2005 and 2023 in their Figure 3. The increase in the population of people over 70 was huge over that 19-year period (35.4 per cent). Over the period 2015 to 2023, the period that might be of most interest in calculating excess deaths, the increase in the population of people over 70 was about 16.8 per cent. This is a substantial change in the very age range within which the bulk of deaths will occur. Consequently, the data within the ONS dataset giving the age profile against month is valuable as a means of taking these changes into account.
The second factor is that on which my suspicions alight. In their previous methodology, the ONS defined the expected number of deaths in 2022 as the average of deaths registered in years 2016, 2017, 2018, 2019 and 2021. For year 2023, they defined expected deaths as the average of years 2017, 2018, 2019, 2021 and 2022. But if one wishes to examine the hypothesis that there has been an increase in excess deaths not directly attributable to covid itself (as opposed to associated interventions), then the baseline must be taken prior to the period in which the hypothesised factor applies. The ONS ‘contaminate’ their baseline with data from post-covid years and this is indisputably inappropriate for the purpose of examining said hypothesis.
Unfortunately, the ONS’s revised methodology has compounded this problem: they now also include the peak covid year, 2020, in their baseline – albeit they omit months April, May, November and December 2020 (and also January, February 2021) due to these being the peaks in covid deaths. Simply put, by including post-covid years, 2020 to 2022, in their baselines, if there is a genuine increase in excess deaths since 2020, and not attributable to covid, then the estimate of this excess would be minimised by including this increase in the baseline before the subtraction which yields the apparent excess death figure.
One is tempted to describe what was done by ONS as ‘baffling’ or ‘incomprehensible’ or ‘preposterous’. However, given that the statisticians carrying out the work are clearly competent, it seems more likely that they simply did not wish to examine the hypothesis of a non-covid health factor causing excess deaths since 2020.
Nerdy Notes for Statisticians
The ONS regression models are fairly ‘plain vanilla’ with linear terms and two quadratic interaction terms (age x sex and age x Trend). The log of the monthly, or weekly, numbers of deaths is regressed, but the inclusion of the log(population) in the model means that this is equivalent to regressing the log of the death rates, per age-sex-geography stratum.
This is a quasi-Poisson regression (variance not constrained to equal the mean). Poisson type regressions are often used with data which counts events (as here). It is not immediately obvious (to me, anyway) whether the regression of log(data) rather than the raw data will lead to a greater, or reduced, extrapolation (i.e. of expected deaths one year later). I explore this in my independent analyses below.
Independent Reanalysis
I have not used the ONS code; I have not used the code ‘R’ at all. Instead I have used Python with statsmodels.api OLS functionality.
However, I have used the same dataset as ONS. As explained above, this offers an improvement on previous datasets because it contains the variation of the UK age profile over the last 19 years.
I initially use the same regression model as ONS, i.e. based on the log of the dependent variable (quasi-Poisson) and the same dependent variables. However, I have restricted my re-analysis to the case of monthly data (not weekly) and have fitted the model to all-UK. This contrasts with ONS where fits were conducted for the four UK nations separately before summing to get the UK total of excess deaths. Hence the model I have used has 111 independent variables.
The ONS uses a baseline for the fitting of the model which varies according to the month in which the excess deaths are to be estimated, and with a 12-month lag. For example, to estimate the excess deaths in January 2023 they fitted the model to data from February 2017 to January 2022 (inclusive), whereas for February 2023 they fitted the model to data from March 2017 to February 2022 (inclusive), etc. This requires a great deal of refitting the model (and that would be even more the case if using weekly data).
I have adopted a shortcut for expediency and speed of response. For the whole of 2023 I have fitted the model to the middle of the range that was used by ONS, namely July 2017 to June 2022 (inclusive).
Readers will appreciate that my concern over the ONS analysis relates to their inclusion of the covid and post-covid years in the baseline, as the above range of fitted dates illustrates. To reiterate the key issue: if one wishes to examine the hypothesis that there has been an increase in excess deaths NOT directly attributable to covid itself (as opposed from associated interventions), then the baseline MUST be taken prior to the period in which the hypothesised factor applies. If instead the ONS approach to the baseline is adopted, any signal in the data that would align with the hypothesis is fully or partially ‘subtracted out’ when the difference is calculated between actual deaths and predicted (i.e. ‘expected’) deaths.
Consequently, I have also deployed the same regression model but fitted it to the five years of data 2015 to 2019, i.e. pre-covid, as the appropriate means of predicting the expected deaths in years 2020 and thereafter.
Actually, with the use of a regression model including time dependent terms (both age profile and the ‘Trend’ variable) the implicit rationale for using only a five-year period as the baseline has ceased to apply. A reasonably short baseline was necessary when a simple average death rate over those years was used, because in that case the baseline should not be too strongly influenced by long-term trends. However, since trends are included in the regression model it is equally (or perhaps more) appropriate to use as the baseline a fit to all the pre-2020 data, i.e., from 2005 to 2019 in the available dataset. I have therefore also considered this definition of the baseline.
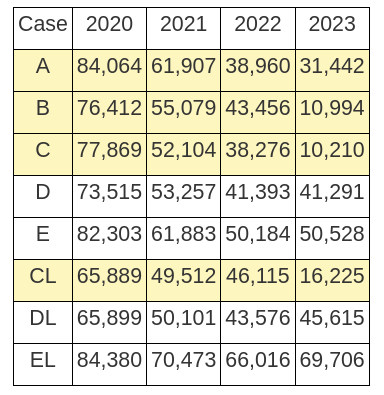
Here I give the results for annual excess deaths in the UK for the following cases.
Models based on the log of the dependent variable
A = ONS results: old method
B = ONS results: new method
C = my approximation of the ONS new method
D = based on the baseline 2015 to 2019 for all predicted years from 2020 onwards
E = based on the baseline 2005 to 2019 for all predicted years from 2020 onwards
Models using death rate as the dependent variable
CL = my approximation of the ONS new method (other than dropping the logarithm)
DL = based on the baseline 2015 to 2019 for all predicted years from 2020 onwards
EL = based on the baseline 2005 to 2019 for all predicted years from 2020 onwards
Note that all results use the ONS regression model, and all results include the changes of age profile over time. They differ only in the definition of the baseline (and, in cases, CL, DL, EL, the use of the death rate as the fitted variable, rather than its logarithm).
The baselines have been defined earlier. One exception is for cases C and CL when predicting year 2022. For these cases I used both a baseline terminating in June 2021 and a baseline terminating in December 2021, and then used the average excess deaths predicted for 2022.
Results are given in Table 1 below. These are best estimates for each model/case.
Table 1: Annual excess deaths, 2020 – 2023. The shaded results, below, cannot be considered to include correctly any post-2020 effects on health, other than deaths from covid itself, due to inappropriate baselines. The unshaded results are my best estimates including any post-2020 effects on health. These are total excess deaths, including deaths due to covid.
Conclusions
1. Both the current and new methods used by the ONS fail to address the hypothesis that there might be unexplained excess deaths post-covid, not attributable directly to covid (as opposed to associated interventions). This failure is due to the use of baselines which are inappropriate for this purpose.
2. Inclusion of covid and post-covid years in the ONS baselines potentially contaminates the baseline with any post-covid health factors via the ‘Trend’ variable (which occurs in the model in both linear and interaction terms).
3. Consequently, the quantity calculated by ONS and called ‘excess deaths’ has no clear interpretation, but is certainly not an excess with respect to what would have been expected prior to covid (even allowing for trends).
4. The ONS model itself, together with the associated dataset, does provide the basis of an improved method for estimating excess deaths. In particular, the inclusion of time-dependent age profiles and the additional ‘Trend’ variable are both important as regards improving extrapolation from pre-covid to post-covid periods.
5. Using the ONS model and baselines which terminate on 31 December 2019, i.e. pre-covid, all the models/cases show excess deaths remain high.
6. Excess deaths in 2023 have not reduced from those in 2022.
7. In as far as deaths attributable to covid reduced from 2022 to 2023, this implies non-covid excess deaths increased in 2023.
8. Central estimates for total annual excess deaths in 2022 or 2023 are in the range 41,000 to 70,000.











